Le dernier billet sur le Go commis sur ce site était un peu ésotérique, surtout pour le non initié d'autant plus qu'il présentait les choses de façon intentionnellement baroque. Je voudrais revenir à des choses plus fondamentales, plus simples, essentielles : les formes élémentaires et leur statut.

Un des points importants au Go d'après mon expérience et d'avoir une idée aussi juste que possible du statut de ses groupes de pierres. Un groupe de pierres peut être tout simplement vivant, mort ou l'un et l'autre à la fois au sens ou bien que vivant et non encore mort seul l'avenir et les capacités relatives des 2 joueurs décidera du statut définitif du groupe.

A noter que le voisinage d'un groupe influe sur son statut. Nous tâcherons d'illuster cela succintement.

Pour vivre, il faut 2 yeux, que ces 2 yeux aient été effectivement formés ou non :

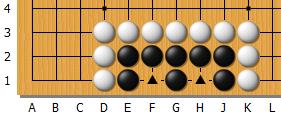
Ci-dessus les intersections marquées d'un triangle au sein du groupe de pierres noires constituent les 2 yeux de ce groupe qui est définitivement vivant : aucun moyen pour Blanc de priver Noir de toutes ses libertés, il faudrait pour cela qu'il joue simultanément dans les 2 yeux, ce qui n'est pas autorisé par les règles.

Observons le presque même groupe, privé d'une pierre :

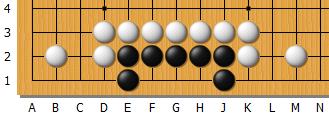
Quel est le statut du groupe. Si Noir joue en 1er sur l'intersection du milieu (intersection G1), il forme 2 yeux et vit. Si Blanc joue sur cette intersection, Noir meurt : c'est le point vital de ce groupe. La séquence artificielle suivante tient lieu de démonstration :

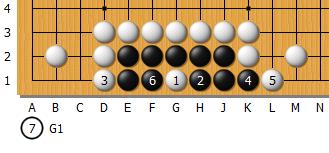
Ce groupe de pierres à 3 intersection est vivant ou mort suivant le trait. Il en est de même pour ce même groupe de 3 intersections :

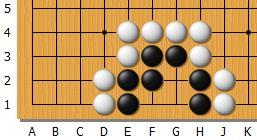
Le point vital de ce groupe est l'intersection G1, point de symétrie qu'on ne manquera pas de considérer lorsqu'on s'évertuera à dénicher le point vital de notre groupe, fébrile, tremblant, tiraillé entre le dégoût de soi et la colère à l'encontre de l'adversaire pour finalement conclure mais sans certitude qu'il n'existe pas, ce point vital et que le Go n'est de toute façon qu'un jeux, un passe-temps comme un autre, une activité dans laquelle on s'absorbe à défaut de s'absorber dans la Vie, la vraie. Puis se re saisissant, l'esprit concentré, débarrassé du pathos, des passions, un point semble luire dans l'ombre...

Changeons un peu la situation :

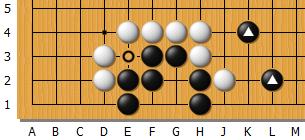
Le groupe noire a une liberté en plus : intersection marquée d'un cercle en E3 et il y a 2 copines à proximité. Dans ces conditions, le point vital de Noir n'est pas encore vital car Blanc a une faiblesse. S'il joue immédiatement en G1 :

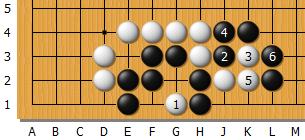
Noir exploite la faiblesse et sans sort. Le voisinage de Noir l'a rendu plus fort : il n'y a pas de nécessité pour Noir de jouer immédiatement sur le point vital qui n'en est pas encore un. 

Le coup B1 du diagramme ci-dessous, en couvrant la faiblesse de Blanc rend l'intersection G1 vitale pour le groupe noir, ce qu'elle n'était pas jusque-là :

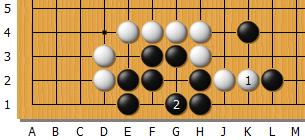
Dans ces exemples, les groupes sont presque formés entièrement, avec des frontières bien tracées. En partie réelle, il ne faut pas attendre que les groupes se dessinent pour les observer, les étudier pour en déterminer le statut, leurs ébauches peut suffir. Les points vitaux apparaissent, un peu flous au début puis de plus en plus nette, parfois ils sont nettes (probabilité maximale) mais ils peuvent se nimber à nouveau dans la brume :

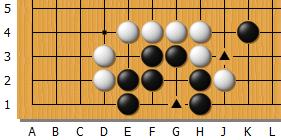
Sans la pierre noire en L2, J3 n'est pas encore une faiblesse pour Blanc et donc G1 est un point vital pour Noir. Si Noir ajoute un pierre en L1, G1 perd sa nature vitale, du moins il ne l'est plus aussi nettement que sans la pierre noire en L3.

Avant d'aller plus loin et pour conclure pour ce soir, illustrons la notion de faux oeil :

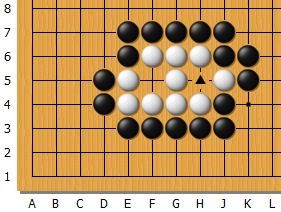
L'intersection marquée d'un triangle est un faux oeil du groupe Blanc qui est pour le coup mort. Celui-ci est relativement simple a diagnostiquer, d'autres sont un peu plus subtiles. La nature véritable d'un oeil est fluctuante, ce sont des probabilités qui évoluent dans le temps, 1 étant une probabilité absorbante, une fois qu'un oeil est vrai rien ne pourra changer sa nature, à la différence du point vital. Rendre les yeux potentiels d'un groupe faux c'est le tuer : si au final il ne lui reste qu'un seul vrai oeil, ce n'est pas suffisant.

J'aborderais ultérieurement en commentaire de ce billet d'autres groupes et leur statut. Vous comprendrez en particulier le titre donné à ce billet. J'ajouterais au gré de ma fantaisie et de l'inspiration du moment quelques remarques qui pourraient je l'espère vous inciter à cheminer sur la voie ardue, parfois ingrate du Go (qui comme toutes ces voies arides est ô combien enrichissante).